¿Qué es el interés simple?
El interés simple se refiere al costo de financiamiento calculado como un porcentaje del capital inicial. Este tipo de interés no considera los intereses acumulados anteriormente; se basa únicamente en el monto principal original. Es ampliamente utilizado en préstamos de consumo y algunos productos de ahorro, como certificados de depósito. Los prestatarios se benefician del interés simple porque solo pagan interés sobre el monto prestado, sin acumular intereses adicionales sobre intereses previos.
El cálculo del interés simple es directo: se multiplica el principal por la tasa de interés y por el tiempo del préstamo o inversión. Por ejemplo, si inviertes 100,000 € a un 7% durante tres años, ganarás 21,000 € en interés simple al final del período.
¿Cuál es la naturaleza del interés simple?
El interés simple se calcula con la siguiente fórmula:
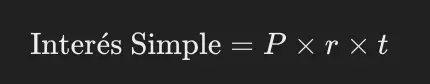
Donde:
- P es el capital principal,
- r es la tasa de interés,
- t es el tiempo.
Si se calcula para un período corto, como días o meses, la tasa de interés debe ajustarse en consecuencia. Por ejemplo, un préstamo de 50,000 € por 60 días con un 5% de interés anual genera 410,95 € en interés simple.
¿Qué es el interés compuesto?
El interés compuesto, a diferencia del simple, acumula intereses sobre el interés generado previamente, además del capital inicial. Esto permite que una inversión crezca a un ritmo acelerado a medida que se reinvierten las ganancias. La frecuencia de capitalización—diaria, mensual, trimestral, etc.—determina cuán rápido se acumulan los intereses, beneficiando así a los inversores.
Por ejemplo, al invertir 10,000 € a un 10% anual durante cinco años, obtendrás 6,105 € en interés compuesto, superando los 5,000 € que generaría el interés simple en el mismo período.
¿Cuál es la naturaleza del interés compuesto?
El interés compuesto se calcula con la fórmula:
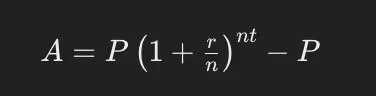
Donde:
- A es el interés compuesto,
- P es el capital principal,
- r es la tasa de interés,
- n es la frecuencia de capitalización,
- t es el tiempo.
Por ejemplo, si la capitalización se realiza semestralmente, el rendimiento al final de cinco años será de 6,289 €, mostrando un beneficio adicional debido a la mayor frecuencia de capitalización.
Períodos de capitalización
Ahora que hemos explorado la fórmula del interés compuesto, es importante entender un elemento clave dentro de esta: los períodos de capitalización. Estos determinan con qué frecuencia se añade el interés ganado al capital inicial, lo cual puede variar de anual a semestral, trimestral, mensual o incluso diario.
Cuanto más frecuente sea la capitalización, mayor será el efecto del interés compuesto, ya que los intereses se añaden al saldo principal con mayor regularidad, generando más intereses en cada nuevo período. Esto puede acelerar significativamente el crecimiento de tu inversión o aumentar el costo de un préstamo. Por lo tanto, al evaluar un producto financiero, es esencial considerar no solo la tasa de interés, sino también la frecuencia de capitalización, ya que esto impacta directamente en los rendimientos o pagos totales.
Otros conceptos de interés compuesto
Después de entender cómo funcionan los períodos de capitalización, es útil explorar otros conceptos clave relacionados con el interés compuesto, como el valor temporal del dinero y la Regla del 72.
Valor temporal del dinero
El valor temporal del dinero nos enseña que un dólar hoy vale más que un dólar en el futuro debido a su potencial para ganar intereses. Este principio es esencial para la toma de decisiones financieras a largo plazo.
Regla del 72
Por otro lado, la Regla del 72 es un método rápido para estimar cuánto tiempo tomará duplicar una inversión con interés compuesto. Simplemente divides 72 por la tasa de interés anual, y el resultado te dará el número de años aproximados necesarios para que tu inversión se duplique. Este concepto es especialmente útil para evaluar la eficiencia de diferentes inversiones sin necesidad de cálculos complejos.
Compound Annual Growth Rate (CAGR)
Tras explorar conceptos fundamentales como el valor temporal del dinero y la Regla del 72, es momento de abordar una métrica clave para medir el crecimiento de las inversiones a largo plazo: la Tasa de Crecimiento Anual Compuesta (CAGR).
El CAGR es una medida que describe la tasa de crecimiento anual promedio de una inversión durante un período específico, considerando los efectos del interés compuesto. Se calcula utilizando la fórmula:
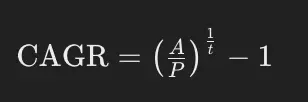
Donde:
- A es el valor final de la inversión.
- P es el valor inicial.
- t es el número de años.
El CAGR es crucial porque permite comparar el crecimiento de diferentes inversiones a lo largo del tiempo, proporcionando una visión clara del rendimiento real, más allá de las fluctuaciones a corto plazo. Es una herramienta indispensable para evaluar la rentabilidad de una inversión de manera consistente y precisa.
Aplicaciones reales
Con todo lo aprendido sobre interés compuesto, es esencial ver cómo estos conceptos se aplican en la vida real.
El interés compuesto es omnipresente, desde las cuentas de ahorro, hasta los fondos de inversión y las hipotecas. Por ejemplo, al invertir en un fondo de inversión, el interés compuesto permite que las ganancias se reinviertan automáticamente, acelerando el crecimiento del capital. Además, en el ámbito de los préstamos, comprender cómo se acumula el interés compuesto te ayuda a evaluar el verdadero costo de una hipoteca o préstamo personal.
Estos ejemplos muestran cómo el interés compuesto puede influir significativamente en tus decisiones financieras cotidianas y a largo plazo.
» ¿Listo para utilizarlo a tu favor? Mejores ETFs de este año.
Consideraciones adicionales sobre los intereses
Ahora que hemos explorado cómo el interés compuesto se aplica en la vida real, es importante considerar algunos factores adicionales al evaluar cualquier producto financiero. Las consideraciones adicionales sobre el interés incluyen entender el impacto de la inflación en el poder adquisitivo de tus rendimientos, los efectos fiscales sobre las ganancias generadas por el interés compuesto y la importancia de comparar las tasas de interés efectivas al analizar diferentes opciones de inversión o financiamiento. Estos factores pueden influir significativamente en la rentabilidad neta y en la viabilidad de tus decisiones financieras.
Conclusión
En resumen, comprender la diferencia entre el interés simple y compuesto, junto con los conceptos clave como la Tasa de Crecimiento Anual Compuesta (CAGR) y la importancia de los períodos de capitalización, te proporciona una base sólida para tomar decisiones financieras informadas.
Al aplicar estos conocimientos en situaciones reales, podrás maximizar el crecimiento de tus inversiones y minimizar el impacto de los costos financieros a lo largo del tiempo. Equipado con esta información, estarás mejor preparado para alcanzar tus objetivos financieros de manera efectiva y estratégica.
» Continúa aprendiendo con: Inversión activa vs inversión pasiva.
