¿Cómo funciona el modelo binomial?
El modelo binomial funciona creando un “árbol de precios” que descompone el tiempo de vida de una opción en una serie de pasos discretos. En cada paso, se asume que el precio del activo subyacente puede moverse hacia arriba o hacia abajo en un porcentaje predeterminado, lo que permite construir un esquema detallado de posibles escenarios futuros. Este enfoque simplifica los cálculos al representar solo dos posibles movimientos por período, pero ofrece un análisis detallado y dinámico del comportamiento del precio.
» Aquí tienes los mejores brokers de opciones
Para calcular el valor de la opción, el proceso comienza por asignar valores a los nodos finales del árbol, los cuales corresponden al valor intrínseco de la opción en su fecha de vencimiento. Luego, se aplica un cálculo hacia atrás, desde los nodos finales hasta el nodo inicial, utilizando probabilidades de movimiento (hacia arriba o abajo) y una tasa de descuento que ajusta los valores futuros al presente. Esto permite estimar el valor de la opción en cada etapa del árbol y, finalmente, determinar su precio teórico en el momento actual.
Este método es especialmente útil porque permite incorporar características específicas de las opciones, como pagos de dividendos o decisiones de ejercicio anticipado. La flexibilidad del modelo binomial lo hace ideal para valorar opciones americanas, donde el titular puede decidir ejercitar la opción en cualquier momento antes de su vencimiento. Esto lo convierte en una herramienta práctica para analizar escenarios reales del mercado.
» Sigue aprendiendo sobre opciones: ¿Qué es un Married Put?.
Cálculos del modelo binomial de valoración de opciones
Después de entender cómo funciona el modelo binomial, es importante profundizar en los cálculos necesarios para valorar tanto call options (opciones de compra) como put options (opciones de venta). Este proceso sigue un enfoque estructurado que integra probabilidades, movimientos del precio del activo subyacente y tasas de descuento para determinar el valor teórico de la opción.
» Aprende con las mejores Frases de Mujeres Millonarias
1. Opciones de compra (Call Options):
Para calcular el precio de una opción de compra, se comienza con el valor intrínseco en los nodos finales del árbol, que se determina como la diferencia entre el precio del activo subyacente y el precio de ejercicio, si es positiva (en caso contrario, el valor es cero). A medida que se retrocede en el árbol, se utiliza la fórmula del valor esperado ajustado por la tasa de descuento:
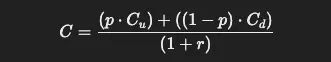
Donde:
- CCC es el valor de la opción en el nodo actual.
- CuC_uCu y CdC_dCd son los valores de la opción en los nodos de subida y bajada, respectivamente.
- ppp es la probabilidad de subida, calculada como:
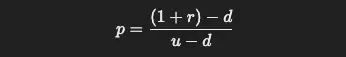
- r es la tasa de descuento, uuu es el factor de subida, y ddd es el factor de bajada.
Este método permite ajustar el valor de la opción según los movimientos del precio del activo y la probabilidad de que estos ocurran.
2. Opciones de venta (Put Options):
Para una opción de venta, el proceso es similar, pero el valor intrínseco en los nodos finales se calcula como la diferencia entre el precio de ejercicio y el precio del activo subyacente, si es positiva (en caso contrario, el valor es cero). Se aplica la misma fórmula de cálculo hacia atrás, ajustando por las probabilidades de movimiento y la tasa de descuento:
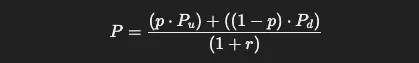
Donde los valores y las probabilidades siguen los mismos cálculos que en las opciones de compra, pero adaptados para reflejar la naturaleza de una opción de venta.
En ambos casos, el modelo binomial proporciona un marco claro y estructurado para calcular el valor de las opciones, incorporando las dinámicas del mercado y las características específicas de cada tipo de contrato. Esto lo convierte en una herramienta esencial para los traders e inversores que buscan tomar decisiones informadas.
Ejemplo del modelo binomial
Después de comprender los cálculos del modelo binomial, un ejemplo práctico puede ayudarte a visualizar cómo se aplican estos pasos. Supongamos una opción de compra (call option) con un precio de ejercicio de 50 € y un activo subyacente que actualmente cotiza a 50 €. La tasa de interés es del 5 %, el tiempo hasta el vencimiento es de un año, y el precio del activo puede subir un 20 % (u=1.2u = 1.2u=1.2) o bajar un 20 % (d=0.8d = 0.8d=0.8).
Paso 1: Construir el árbol de precios
En el primer período, el precio del activo puede subir a 60 € (50 € × 1.2) o bajar a 40 € (50 € × 0.8). Si sube, en el segundo período los valores posibles serán 72 € (60 € × 1.2) o 48 € (60 € × 0.8). Si baja, los valores serán 48 € (40 € × 1.2) o 32 € (40 € × 0.8). Este árbol binomial muestra todos los escenarios posibles del precio del activo hasta el vencimiento.
Paso 2: Calcular el valor de la opción
Para los nodos finales:
- Si el precio es 72 €, el valor de la opción será 22 € (72 € – 50 €).
- Si el precio es 48 €, la opción no tendrá valor, ya que no se ejercería.
- Si el precio es 32 €, la opción tampoco tendrá valor.
Trabajando hacia atrás en el árbol, se calcula el valor de la opción en cada nodo anterior usando la fórmula:
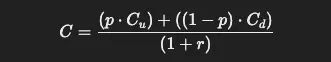
Donde ppp es la probabilidad de subida ajustada por el riesgo. Finalmente, se obtiene el valor de la opción en el nodo inicial.
Este ejemplo ilustra cómo el modelo binomial proporciona una visión detallada y estructurada para valorar opciones financieras, permitiéndote analizar cada posible escenario de mercado. Es una herramienta clave para planificar tus estrategias de inversión.
Ventajas y desventajas del modelo binomial
Después de analizar cómo funciona el modelo binomial y sus aplicaciones prácticas, es importante entender sus principales ventajas y desventajas. Para facilitar la lectura, aquí tienes una tabla comparativa que resume los aspectos clave:
| Ventajas | Desventajas |
|---|---|
| Flexibilidad: Se adapta a opciones americanas y europeas, permitiendo modelar ejercicios anticipados. | Complejidad creciente: Aumenta significativamente con más pasos, lo que puede requerir mayor potencia computacional. |
| Capacidad de personalización: Permite incorporar dividendos, volatilidad variable y otros factores específicos. | Menos intuitivo que otros modelos: Puede ser más difícil de entender para principiantes. |
| Precisión ajustable: Más pasos en el árbol mejoran la precisión del resultado. | Menor eficiencia para opciones complejas: En casos muy específicos, como derivados exóticos, otros modelos pueden ser más adecuados. |
| Cálculos estructurados: Ofrece una metodología clara y paso a paso para valorar opciones. | Asume simplicidad en los movimientos del precio: Solo considera dos movimientos por período, lo que puede limitar escenarios más complejos. |
| Útil para decisiones estratégicas: Ayuda a los traders a visualizar escenarios futuros y planificar estrategias. | Dependencia de parámetros estimados: La precisión depende de la exactitud de los factores como volatilidad y tasas de interés. |
Modelo binomial de valoración de opciones vs. modelo Black-Scholes
El modelo binomial y el modelo Black-Scholes son dos herramientas ampliamente utilizadas para valorar opciones financieras, pero tienen diferencias clave que los hacen adecuados para distintas situaciones. El modelo binomial se basa en una estructura de pasos discretos, descomponiendo el tiempo en períodos y modelando movimientos hacia arriba o hacia abajo en cada paso, lo que lo hace ideal para valorar opciones americanas, donde el ejercicio anticipado es una posibilidad. Por otro lado, el modelo Black-Scholes asume un tiempo continuo y utiliza una fórmula matemática cerrada, lo que lo hace más rápido para calcular opciones europeas, donde el ejercicio solo se realiza al vencimiento.
Una de las ventajas principales del modelo binomial es su flexibilidad. Permite incorporar pagos de dividendos, volatilidad cambiante e incluso ajustar los cálculos para activos que no se comportan de forma lineal. En cambio, el modelo Black-Scholes, aunque más simple y directo, asume una volatilidad constante y no contempla ejercicios anticipados, limitando su aplicación en escenarios donde las condiciones del mercado son más dinámicas.
En resumen, el modelo binomial es más detallado y adaptable, pero requiere mayor esfuerzo computacional. Por otro lado, el modelo Black-Scholes es ideal cuando se busca rapidez y se trabaja con opciones europeas. Elegir entre uno y otro depende de las características específicas de la opción y del nivel de precisión y personalización que se necesite en el análisis.
» Sigue aprendiendo: Opciones de bonos
Modelo binomial de valoración de opciones vs. modelo Monte Carlo
El modelo binomial y el modelo Monte Carlo son dos enfoques diferentes para valorar opciones financieras, y cada uno tiene ventajas específicas dependiendo del contexto. El modelo binomial utiliza un árbol de precios que descompone el tiempo en pasos discretos, lo que permite modelar opciones con ejercicios anticipados, como las opciones americanas. En cambio, el modelo Monte Carlo se basa en simulaciones aleatorias para generar miles de posibles trayectorias del precio del activo subyacente, lo que lo hace especialmente útil para opciones más complejas o derivados exóticos.
Una de las principales diferencias radica en la precisión y el esfuerzo computacional. El modelo binomial es preciso y estructurado, pero puede volverse complicado si se necesitan muchos pasos para lograr resultados detallados. Por su parte, el modelo Monte Carlo es ideal para escenarios con múltiples variables o donde los precios de los activos tienen comportamientos no lineales. Sin embargo, la precisión del modelo Monte Carlo depende del número de simulaciones realizadas, lo que puede aumentar significativamente el tiempo de cálculo.
En resumen, el modelo binomial es más adecuado para opciones tradicionales y situaciones donde el ejercicio anticipado es importante, mientras que el modelo Monte Carlo brilla en la valoración de productos financieros complejos y escenarios con incertidumbre elevada. Elegir entre ambos dependerá del tipo de activo que se valore y de la capacidad para manejar cálculos más intensivos o detallados.
Conclusión
El modelo binomial de valoración de opciones es una herramienta clave para entender el precio de las opciones financieras y tomar decisiones informadas. Su capacidad para descomponer el tiempo en pasos discretos y modelar escenarios detallados lo convierte en un método esencial para valorar tanto opciones de compra como de venta, especialmente aquellas con ejercicios anticipados. Si bien tiene sus limitaciones frente a modelos como Black-Scholes o Monte Carlo, su flexibilidad y precisión ajustable lo hacen indispensable para quienes buscan profundizar en el análisis financiero.
Si estás interesado en seguir explorando conceptos avanzados, no te pierdas nuestro siguiente artículo sobre opciones sintéticas, una estrategia que combina instrumentos financieros para replicar posiciones de activos. Es el complemento perfecto para expandir tus conocimientos y diversificar tus herramientas en el mundo de las opciones. ¡Nos vemos allí!








